Bijvoet-Pair Analysis and Bayesian Statistics

This routine offers a detailed analysis of the Bijvoet (Friedel) pairs found in an Fo/Fc reflection CIF, both as a Scatter Plot and in terms of Bayesian Statistics, to establish the absolute structure in terms of the Hooft parameter. Details on the theory behind the Hooft parameter can be found in
J. Appl. Cryst. (2008), 41, 96-103, [Hooft, Straver & Spek].
See also Rob Hooft's Website on Absolute Structure Determination."

Required data are a .cif and an .fcf (including Friedel (Bijvoet) related reflection pairs) for the non-centrosymmetric structure. The structure factors that are used in the analysis are by default re-calculated from the parameter data in the .cif file. Alternatively, calculated structure factors can be taken from the .fcf by setting an appropriate switch (see warning below!).

Note: When the F(calc) values are choosen to be taken from the .fcf, that file should NOT be based on a BASF/TWIN refinement. Flack parameter contributions to F(calc) are incorperated by SHELXL-97 into the .fcf with a BASF/TWIN refinement, making them useless for this application. That is not the case with the default Flack parameter (hole-in-one) determination.

Note: The currently most used standard procedure for the determination of the absolute structure with X-ray diffraction techniques is based on the determination of the Flack parameter with its associated standard uncertainty as part of the least-squares refinement procedure (preferably with the BASF/TWIN instructions). The alternative post-refinement procedure that is implemented in PLATON (based on a theory developed by Dr. Rob Hooft) addresses in particular those marginal cases of relatively weak resonant power of enantiopure compounds where the results of the Flack analysis are inconclusive (the results of both procedures are consistent in cases of sufficient resonant power).

Comparison of the Flack and Bayesian Statistics approach.

The Flack parameter can be estimated as part of the least squares refinement procedure even in the absence of any Friedel Pair. It has been shown that in such a case correlation may systematically affect its value and the positional parameters. The Hooft procedure explicitly needs sufficient Friedel Pair coverage in order to work. The values of the Flack and Hooft parameter are generally in agreement given sufficient Friedel coverage. The associated standard uncertainty of the latter is generally half of the former one.

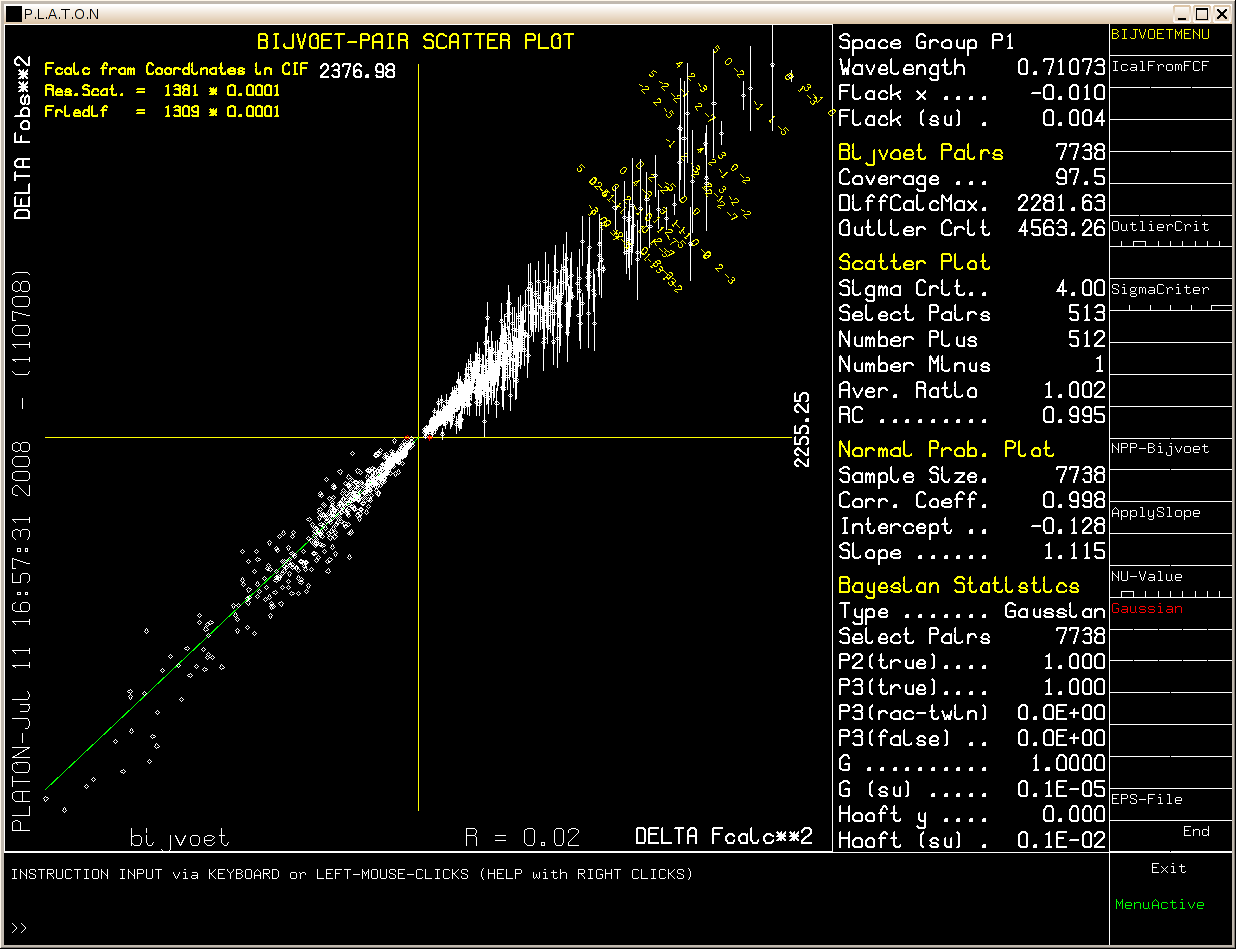
Example of a Heavy Atom Structure in P1

Example: [Flack x = -0.010(4), abs[F1(calc)**2 - F2(calc)**2] > 4 Sigma]

Scatter Plot

Calculated Bijvoet differences (Horizontal) are plotted against observed Bijvoet differences (Vertical). Vertical bars indicate one Sigma spread on the observed difference. Reflection indices are displayed for the the strongest Bijvoet differences. Bijvoet pairs for which the observed and calculated differences have the same sign are shown in white and those with opposite signs in red.

Only the 513 Bijvoet differences above the selectable sigma level (4 * Sigma in this example) are displayed in the scatter plot out of the total number of 7738 Bijvoet pairs.

Sigma = sqrt(sigma**2(F1(obs)**2) + sigma**(F2(obs)**2)), where F1 and F2 represent the Friedel (Bijvoet) related reflections.

Plot entries are expected to be located in the upper right (or inversion related lower left) quadrant for the correct absolute structure. Deviating entries (i.e. located in the other two quadrants) are in red. A least squares line (green) is calculated through the points. This line is expected to run from the lower left to the upper right corner for the correct absolute assignment. A change to the opposite absolute structure is indicated when this line runs from the upper left to the lower right corner. All except one of the 513 pairs that meet the 4*Sigma criterium confirm the selected absolute structure (given that the compound is enantiopure).

The Average Ratio parameter is expected to have a value close to 1.0 for a strongly determined absolute structure and is defined as:

Sum(weight((Fo1**2-Fo2**2)/(Fc1**2-Fc2**2))) / Sum(weight)

with: weight = abs(Fc1**2-Fc2**2) / sigma

More details can be found in the listing file.

Bayesian Statistics

An alternative analysis of the absolute structure is provided under the heading Bayesian Statistics.

Three types of analysis are done:

The value of Hooft(Su) is to be compaired with the value of Flack(su).

P2(true) gives the probability (scale 0 to 1) that the current absolute structure is the correct one, assuming that the compound is enantiopure.

The Friedel Coverage is defined as the ratio of the number of Friedel pairs in the data set and the maximum possible number * 100%.

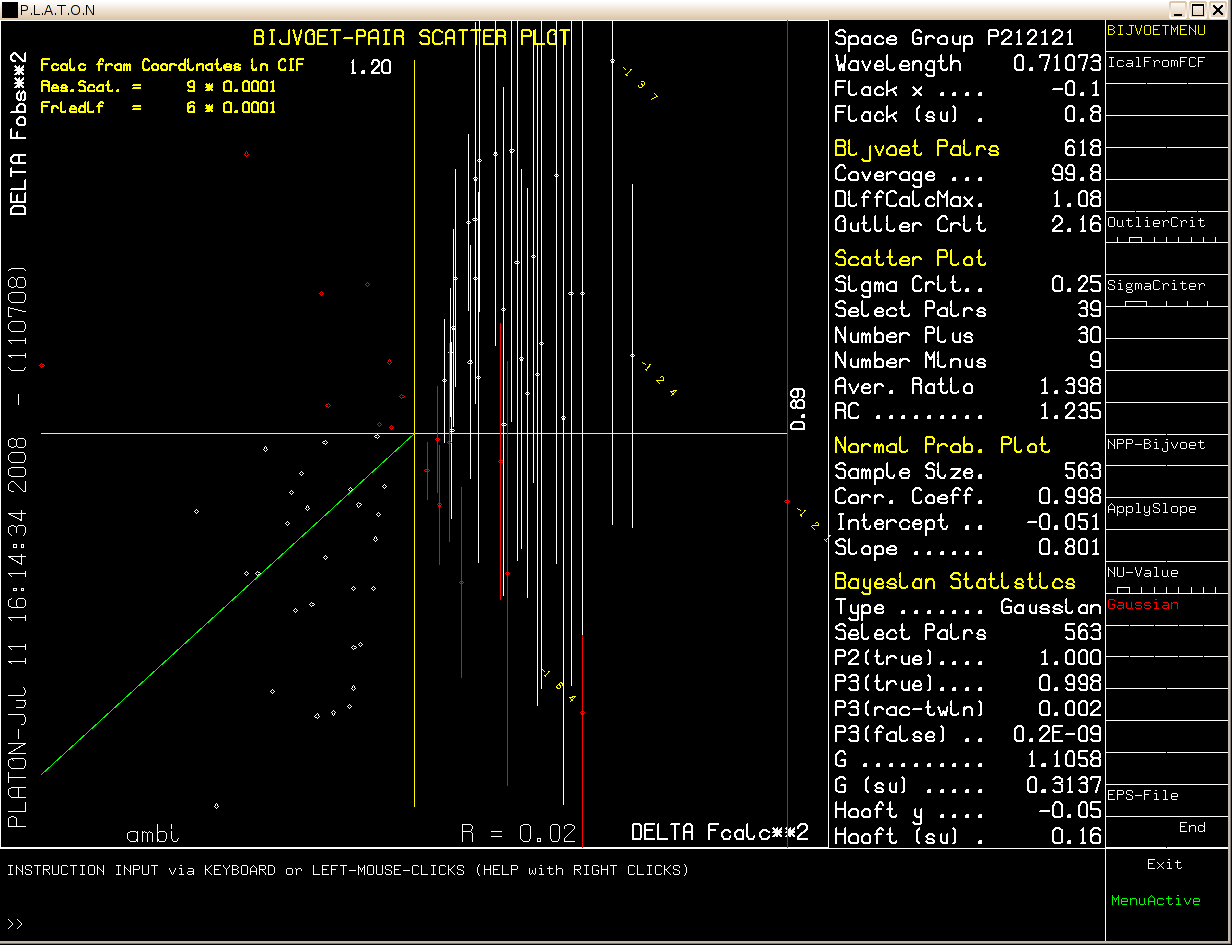
Example of a Light Atom Structure in P212121

Note that the MoKa diffraction data used here are for the Ammonium Hydrogen Tartrate test crystal (Nonius) of known absolute configuration. The Friedel pair coverage is 99.8 %. The sigma selection criterium has to be set rather low in this case (0.25 * Sigma). The P2 value indicates a very probability that the absolute configuration is indeed correctly assigned.

Concluding remarks

It is advised to base the analysis on data with close to 100% Friedel coverage and ion a fully refined structure. Having said that, it turns out that, in our experience, an analysis in the early isotropic refinement stage already predicts the correct absolute structure.

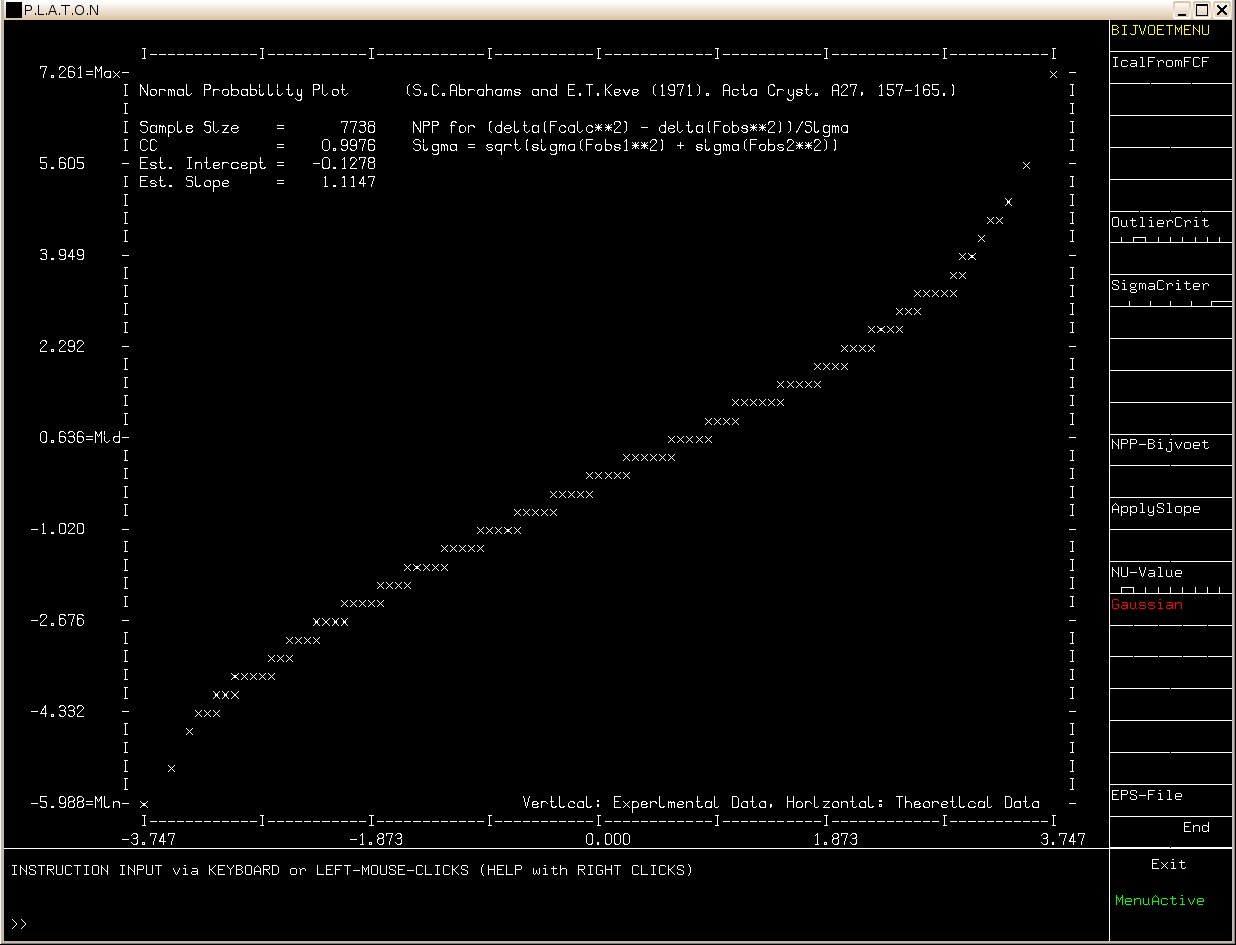
The default analysis assumes a Gaussian error distribution. The validity of this assumption can be tested with a Normal Probability plot (below).

REPORT TOOLS PLATON HOMEPAGE

11-Jul-2008 A.L.Spek